Functions
double	face_number (Polygon f, TTessel *t)
	Return 1. More...

double	face_area_2 (Polygon f, TTessel *t)
	Return the squared face area of a tessellation face. More...

double	face_perimeter (Polygon f, TTessel *t)
	Return the perimeter of a tessellation face. More...

double	face_sum_of_angles (Polygon f, TTessel *t)
	Measure the deviation of a T-tessellation face from a rectangle. More...

double	min_angle (Polygon f, TTessel *t)
	Return the smallest angle in a tessellation face. More...

double	segment_size_2 (std::vector< Point2 > s, TTessel *t)
	Return the squared number of edges on a segment of a T-tessellation. More...

Detailed Description

Functions that can be used by Energy objects for defining a Gibbs model of T-tessellation. Features are measured on vertices, edges, faces or segments.

Function Documentation

double face_area_2	(	Polygon	f,
		TTessel *	t
	)

Return the squared face area of a tessellation face.

Parameters

f	: tessellation face as a polygon.
t	: the tessellation to be considered.

double face_number	(	Polygon	f,
		TTessel *	t
	)

Return 1.

Parameters

f	a polygon representing a tessellation face.
t	the tessellation to be considered.

Silly function that can be used by an Energy object for specifying the number of tessellation face as a feature.

double face_perimeter	(	Polygon	f,
		TTessel *	t
	)

Return the perimeter of a tessellation face.

Parameters

f	: tessellation face as a polygon.
t	: the tessellation to be considered.

double face_sum_of_angles	(	Polygon	f,
		TTessel *	t
	)

Measure the deviation of a T-tessellation face from a rectangle.

Parameters

f	: T-tessellation face as a polygon.
t	: the T-tessellation to be considered.

Only vertices where incident edges form an acute angle contribute to the measure. The additive contribution of such a vertex 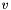$v$ is

$\frac{\pi}{2}-\phi(v),$

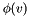where $\phi(v)$ is the (acute) angle between the edges incident to 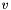$v$ . The above contribution is close to zero if the incident edges are almost perpendicular. It is close to 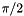$\pi/2$ if the edges are almost aligned.

double min_angle	(	Polygon	f,
		TTessel *	t
	)

Return the smallest angle in a tessellation face.

Parameters

f	: tessellation face as a polygon.
t	: the tessellation to be considered.

Angles between consecutive edges are considered. This function can be used by an Energy object for specifying the sum of face smallest angle as a feature. That feature is of interest for penalizing faces with small angles.

double segment_size_2	(	std::vector< Point2 >	s,
		TTessel *	t
	)

Return the squared number of edges on a segment of a T-tessellation.

Parameters

s	: a T-tessellation segment as a vector of its vertices.
t	: the T-tessellation to be considered.

Function that can be used by an Energy object for specifying the sum of squared number of edges on all segments as a feature. This feature can be used for controlling the variability of segment sizes (here number of edges per segment).