This short tutorial shows how to simulate a given Gibbs model of T-tessellation. The simulation algorithm is described the in paper "A completely random T-tessellation model and Gibbsian extensions". It is a Metropolis-Hastings-Green algorithm. Three main ingredients are involved in the simulation:

A dynamic T-tessellation. That is a T-tessellation that can evolve with time.
A Gibbs model specified by an energy function. T-tessellation with low energy are more likely.
A simulation engine that make the dynamic T-tessellation evolve according to the specified model. The series of T-tessellations generated by the algorithm is a Markov chain of T-tessellations that converges in law to the target distribution.

Below is the whole program. Comments about its different parts follow.

#include ttessel.h
int main(int argc,char** argv) {
  int seed = 5;               // seed for the random generator
  double width = 1;           // side length of the square domain to be tessellated
  double theta_segs = 3.15;   // first parameter value
  double theta_faces = 10000; // second parameter value
  TTessel tes; 
  tes.insert_window(Rectangle(Point2(0,0),Point2(width,width)));
  Energy mod;
  mod.add_features_segs(is_segment_internal);
  mod.add_theta_segs(theta_segs);
  mod.add_features_faces(face_area_2);
  mod.add_theta_faces(theta_faces);
  mod.set_ttessel(tes);
  std::cout << "Current energy: " << mod.get_value() << std::endl;
  SMFChain sim = SMFChain(&mod,0.33,0.33); 
  rnd = new CGAL::Random(seed);
  for(int i=0;i!=100;i++) {
    sim.step();
    std::cout << "Current energy: " << mod.get_value() << std::endl;
  }
return 0;
}

Create a dynamic T-tessellation object

A dynamic T-tessellation is represented by a TTessel object.

TTessel tes;

Before it is really effective, one should define the domain to be tessellated. It must be a bounded convex polygon. Here it is a square window.

tes.insert_window(Rectangle(Point2(0,0),Point2(width,width)));

Define the Gibbs model to be simulated

A stochastic model of T-tessellation is defined through an energy function. For a given energy function 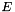$E$ , the infinitesimal probability to observe a T-tessellation 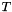$T$ is

$P(dT) \propto \exp\left(-E(T)\right).$

Using Energy objects, one may define a large class of parametric models. As an example, consider the model where the energy function has the form:

$E_\theta(T) = \stackrel{\circ}{n}_\mathrm{s}(T)\theta_1+a^2(T)\theta_2,$

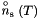where $\stackrel{\circ}{n}_\mathrm{s}(T)$ is the number of tessellation segments not lying along the domain boundary and 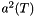$a^2(T)$ is the sum of squared cell areas. Observe that the first term of the energy penalizes T-tessellations with too many segments (cells), while the second term penalizes T-tessellation with heterogeneous cell areas. The numerical values of the parameters are the following:

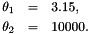
$\begin{eqnarray*} \theta_1 & = & 3.15,\\ \theta_2 & = & 10000. \end{eqnarray*}$

Let us push the first energy term into the model. The number of internal segments can be written as

$\left(\sum_{s\in S(T)} I\{s\mbox{ is internal}\}\right),$

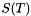where $S(T)$ is the set of segments of the tessellation 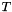$T$ . The following piece of code push this term into the model.

Energy mod;
mod.add_features_segs(is_segment_internal);
mod.add_theta_segs(theta_segs);

The handling of the second term is similar. The sum 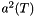$a^2(T)$ of squared cell areas can be written as

$\sum_{c\in C(T)} a(c)^2,$

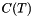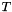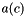where $C(T)$ is the set of cells (i.e. faces) of the tessellation $T$ and $a(c)$ is the area of the cell $c$ .

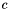mod.add_features_faces(face_area_2);
mod.add_theta_faces(theta_faces);

Now attach the dynamic T-tessellation object to the model object and evaluate the model energy for the current T-tessellation (empty tessellation).

mod.set_ttessel(tes);
std::cout << "Current energy: " << mod.get_value() << std::endl;

Set up the simulator and run it

The class SMFChain implements a simulation engine. It is an algorithm of Metropolis-Hastings-Green type defining a Markov chain in the space of T-tessellations. Transitions of the Markov chain are either merges, splits of flips (SMF). When defining a SMFChain object, one needs to specifiy 2 probabilities : probability of proposing a merge, probability of proposing a split (the third probability for flips is complementary). Very often, these probabilities are chosen uniform.

SMFChain sim = SMFChain(&mod,0.33,0.33);

We are now ready for running the simulator through its method SMFChain::step. As a prerequisite, the random generator must be initialized.

rnd = new CGAL::Random(seed);
for(int i=0;i!=100;i++) {
  sim.step();
  std::cout << "Current energy: " << mod.get_value() << std::endl;